Multitasking Bayesian optimization(MBO)

	贝叶斯优化是一种用于全局优化噪声、代价昂贵的黑盒函数的通用框架。该方法可以使用相对廉价的概率模型去代理财务、计算或物理上昂贵的函数评价。贝叶斯规则用于推导给定观测值的真实函数的后验估计，然后使用代理确定下一个最有希望查询的点。一种常见的方法是使用GP定义从输入空间到希望最小化损失的目标函数的分布。也就是说，给定形式的观察序列对：$\left \{ x_n,y_n \right \}^N_{n=1}$，这里$x_n\in \chi,y_n\in \mathbb{R}$，我们假设f(x)用一个高斯过程来刻画，这里$y_n\sim N(f(x_n),v)$并且$v$是一个函数观测的噪声误差。		

	一种标准的方法是通过查找函数$a(x;\left \{x_n,y_n\right\},\theta)$在定义域$\chi$上的最大值来选择下一个点。期望改进标准(EI)： $$ a_{EI}(x;\left\{ x_n,y_n \right\},\theta)=\sqrt{\sum(x,x;\left\{ x_n,y_n \right\},\theta)}(\gamma(x)\Phi(\gamma(x))+N(\gamma(x);0,1)) $$

	与启发式获取函数(如EI)相比，另一种方法是考虑函数的最小值上的分布，并迭代地评估最能降低该分布熵的点。这种熵搜索策略[18]对降低优化过程中最小值位置的不确定性有很好的解释。在这里，我们将熵搜索问题表示为从预先指定的候选集中选择下一个点。设置一个C个点的集合$\tilde{\mathbf{X}} \subset \mathcal{X}$，我们可以写出一个在$\tilde{\mathbf{X}}$中函数值最小的点$\mathrm{x} \in \tilde{\mathrm{X}}$的概率： $$ \operatorname{Pr}\left(\min \text { at } | \theta, \tilde{\mathbf{X}},\left\{\mathbf{x}_{n}, y_{n}\right\}_{n=1}^{N}\right)=\int_{\mathbb{R}^{C}} p\left(\mathbf{f} | \mathbf{x}, \theta,\left\{\mathbf{x}_{n}, y_{n}\right\}_{n=1}^{N}\right) \prod_{\tilde{\mathbf{x}} \in \tilde{\mathbf{X}} \backslash \mathbf{x}} h(f(\tilde{\mathbf{x}})-f(\mathrm{x})) \mathrm{d} \mathbf{f} $$
	这里$\mathbf{f}$是点$\tilde{\mathbf{X}}$的函数值向量，$h$是Heaviside阶跃函数。如果在x上的y 值被揭示，熵搜索过程依赖于对该分布的不确定性减少的估计。进行以下定义：$\operatorname{Pr}\left(\min \text { at } x | \theta, \tilde{\mathbf{X}},\left\{\mathbf{x}_{n}, y_{n}\right\}_{n=1}^{N}\right)$ as $\mathrm{P}_{\mathrm{min}}$，$p\left(\mathbf{f} | \mathbf{x}, \theta,\left\{\mathbf{x}_{n}, y_{n}\right\}_{n=1}^{N}\right)$ as $p(\mathbf{f} | \mathbf{x})$，高斯过程（GP）似然函数为$p(y | \mathrm{f})$。定义P的熵为$H(\mathbf{P})$。目标是从一组候选点中找出x点，使信息增益在最小位置分布上最大化， $$ a_{\mathrm{KL}}(\mathrm{x})=\iint\left[H\left(\mathrm{P}_{\min }\right)-H\left(\mathrm{P}_{\min }^{y}\right)\right] p(y | \mathrm{f}) p(\mathrm{f} | \mathrm{x}) \mathrm{d} y \mathrm{df} $$
	这里$\mathrm{P}_{\mathrm{min}}^{y}$表明幻想观测$\{x, y\}$已经添加到观察集里。虽然上式没有一个简单的形式，但是我们可以用蒙特卡罗方法通过采样f来近似它。这个公式的另一种替代方法是考虑相对于均匀基分布的熵的减少，但是我们发现公式(7)在实际中工作得更好。

	在多任务GPs框架下，对相关任务进行优化是相当直接的。我们只是把未来的观察限制在感兴趣的任务上，然后像往常一样继续下去。一旦我们对感兴趣的任务有了足够的观察，就可以进行适当的估计$K_{t}$，然后其他任务将作为额外的观察，不需要任何额外的功能评估。图1给出了多任务GP与单任务GP的对比及其对EI的影响。 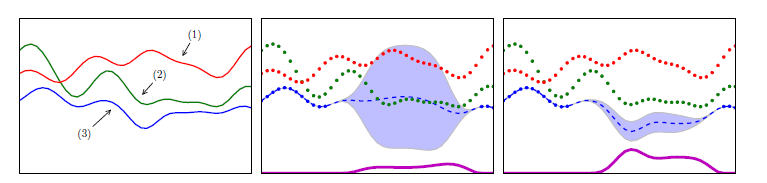![在这里插入图片描述](https://img-blog.csdnimg.cn/20191025195839334.png) 图1 (a)一个包含来自多任务GP的三个任务的示例函数。任务2和任务3是相关的，任务1和任务3是反相关的，任务1和任务2是不相关的。(b)独立的。(c)第三个任务的多任务预测。点表示观察值，虚线表示预测平均值。这里我们展示了三个任务和相应的观察值，目标是最小化第三个任务。底部显示的曲线代表了该任务上每个输入位置的预期改进。独立的GP不能很好地表达函数，优化EI会导致错误的评价。多任务GP利用其他任务，最大EI点对应于真实的最小化。

	在这里，我们将考虑在多个任务上优化平均函数。这包含了单任务和多任务设置的元素，因为我们有一个表示多个任务上的联合函数的目标。我们通过考虑k-fold交叉验证上的更细化的贝叶斯优化来激活这种方法。我们希望优化所有k次折叠的平均性能，但是为了确定考虑中的超参数的质量，可能没有必要实际评估所有这些性能。平均目标的预测均值和方差为: $$ \overline{\mu}(\mathrm{x})=\frac{1}{k} \sum_{t=1}^{k} \mu\left(\mathrm{x}, t ;\left\{\mathrm{x}_{n}, y_{n}\right\}, \theta\right), \quad \overline{\sigma}(\mathrm{x})^{2}=\frac{1}{k^{2}} \sum_{t=1}^{k} \sum_{t^{\prime}=1}^{k} \Sigma\left(\mathrm{x}, \mathrm{x}, t, t^{\prime} ;\left\{\mathrm{x}_{n}, y_{n}\right\}, \theta\right) $$
	如果我们愿意为我们查询的每个点x花费一个函数评估，那么这个目标的优化可以使用标准方法进行。然而，在许多情况下，这可能是昂贵的，甚至可能是浪费。作为一个极端的例子，如果我们有两个完全相关的任务，那么每个查询花费两个函数计算不会提供额外的信息，其代价是单任务优化的两倍。更有趣的情况是，尝试联合选择x和任务t，并且每个查询只花费一个函数评估。

	我们选择$\mathrm{a}(\mathrm{x}, t)$使用两步启发式配对。首先，我们利用预测方法估算缺失的观测值。然后利用估计平均函数选择一个有希望的候选x对EI进行优化。以x为条件，然后我们选择产生最高的单任务预期改进的任务。

	有一种研究多任务平均误差最小化的方法是应用贝叶斯优化来优化多个数据集上的单个模型。他们的方法是将每个函数投射到一个联合的潜在空间中，然后依次迭代地访问每个数据集。

	与其从一个已经完成的相关任务的搜索中转移知识来引导一个新的任务，更可取的策略是让优化例程动态地查询相关的任务，这可能会大大降低成本。直观地说，如果两个任务紧密相关，那么评估一个更便宜的任务可以揭示信息，并减少关于更昂贵任务上最小值位置的不确定性。例如，一个聪明的策略可以在冒险评估一个昂贵的任务之前，对一个有希望的位置进行低成本的探索。在本节中，我们为这种动态多任务策略开发了一个获取函数，该函数特别考虑了基于熵搜索策略的噪声估计成本。虽然EI准则在单个任务用例中是直观有效的，但它不能直接推广到多任务用例中。然而，熵搜索可以很自然地转化为多任务问题。在这种情况下，我们有来自多个任务的观察对$\left\{\mathrm{x}_{n}^{t}, y_{n}^{t}\right\}_{n=1}^{N}$并且选择一个候选的$\mathbf{x}^{t}$，它最大程度地降低了主要任务的$\mathrm{P}_{\mathrm{min}}$的熵，这里我们设置$t=1$。对于$x^{t>1}$而言，$\mathrm{P}_{\mathrm{min}}$评估为0。然而对于$y^{t>1}$，我们可以评估$\mathrm{P}_{\mathrm{min}}^{y}$，并且如果辅助任务与主任务相关，$\mathrm{P}_{\mathrm{min}}^{y}$会改变基本分布并且$H\left(\mathrm{P}_{\min }\right)-H\left(\mathrm{P}_{\min }^{y}\right)$是正的。降低f的不确定性，对相关辅助任务的观测值进行评价可以降低$P_{min}$对感兴趣的主要任务的熵。但是，请注意，在相关任务上评估一个点永远不会比在感兴趣的任务上评估相同的点揭示更多的信息。因此，上述策略永远不会选择评估相关的任务。然而，当考虑到成本时，辅助任务每单位成本可能传递更多的信息。因此，我们将目标由式(6)转化为反映评价候选点的单位成本信息增益： $$ a_{\mathrm{IG}}\left(\mathrm{x}^{t}\right)=\iint\left(\frac{H\left[\mathrm{P}_{\min }\right]-H\left[\mathrm{P}_{\min }^{y}\right]}{c_{t}(\mathrm{x})}\right) p(y | \mathrm{f}) p\left(\mathrm{f} | \mathrm{x}^{t}\right) \mathrm{d} y \mathrm{df} $$ 这里$c_{t}(\mathrm{x}), c_{t} : \mathcal{X} \rightarrow \mathbb{R}^{+}$为计算任务t在x处的实值成本，虽然我们事先不知道这个成本函数，但是我们可以用类似于任务函数的方法来估计它，$f\left(\mathbf{x}^{t}\right)$*：*使用相同的多任务GP机制对$\log c_{t}(\mathrm{x})$进行建模。 ![在这里插入图片描述](https://img-blog.csdnimg.cn/20191025195912151.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzQwNDM0NDMw,size_16,color_FFFFFF,t_70) 图2：一个可视化的多任务信息增益每单位成本的获取函数。在每个图中，目标是求出实蓝色函数的最小值。绿色函数是辅助目标函数。在每个图的底部都有一些线，表示关于主要目标函数的预期信息增益。绿色虚线表示通过评估辅助目标函数得到的关于主要目标的信息增益。图2a显示了来自GP的两个不相关的采样函数，评估主要目标可以获得信息，而评估辅助目标则不能。图2b我们看到，在两个强相关函数的作用下，对其中一个任务的观察不仅减少了对另一个任务的不确定性，而且来自辅助任务的观察获得了关于主任务的信息。最后，在2c中，我们假设主要目标的成本是辅助任务的三倍，因此评估相关任务在单位成本上获得了更多的信息收益。

	图2使用两个任务示例提供了此获取函数的可视化。它展示了如何在相关辅助任务上选择一个点，以减少有关感兴趣的主要任务上的最小值位置的不确定性(蓝色实线)。在本文中，我们假设计算$a_{\mathrm{IG}}$的所有候选点都来自一个固定子集。