Multifactorial Evolutionary Algorithm (MFEA)
闲话:由于前段时间一直忙着写论文,所以很久没有更新了,之前的多目标优化系列我也不打算更新了,因为田野老师的PlatEMO真的很好用,代码也很规范,刚入门的同学们,我很建议你们去看看PlatEMO的源代码,会大有益处。最近看了很多关于多任务优化的文章,觉得这是一个蛮有意思的方向,想把里面最经典的两个方法介绍给大家,今天先介绍第一个MFEA,这个方向有一个平台,这里面有原作者的代码及最新的出版物,感兴趣的同学可以看看:http://www.bdsc.site/websites/MTO/index.html。
一、简介
多任务优化是研究同时解决多个优化问题(任务)从而独立的提高解决每个任务的性能。它的工作原理是假设在解决某个任务时存在一些共同的有用知识,那么在解决此任务的过程中获得的有用知识,可能有助于解决另一个与其有关联的任务。在实际应用中,相关的优化任务是普遍存在的。实际上,其充分利用了基于种群搜索的隐式并行性。
事实上,一个进化多目标优化(EMOO)问题只包含一个任务,该任务可以被求解生成一组Pareto最优解。与此相对,进化多任务优化(EMTO)问题包含多个任务(单目标或多目标),可以同时求解这些任务的最优解。EMTO的目标是利用基于种群的搜索的隐式并行性来挖掘多个任务之间潜在的遗传互补性,EMOO则试图有效地解决同一任务的竞争目标之间的冲突。
给定一个带有k个分量任务的MTO问题,在不失一般性的前提下,我们假设所有组件任务都是单目标、无约束的最小化问题。第j个子任务定义为$T_j$,其对应的目标函数为$f_j:X_j\rightarrow R$,这里$X_j$是一个$D_j$维的解空间,$R$代表实数域,*:*MTO的目标是为每个k分量任务找到全局最优值,即 $$ x_j^o=argmin_{x\in X_j}f_j(x),j=1,...,k $$ 注意,如果对其中特定任务的解空间施加了某些约束,则会将一些约束函数与该任务的目标函数一起考虑。此外,如果组件任务的目标函数是多目标的,MTO将解决多个多目标优化(MOO)问题。
为了说明多目标优化和多任务优化的区别,以下以一个例子说明二者的区别,考虑一个两因素的问题,如图1所示。 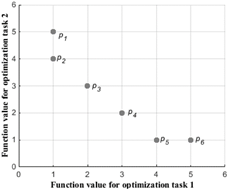
在多目标优化中,$\left{p_2,p_3,p_4,p_5\right}$是第一等级的非支配前沿,$\left{p_1,p_6\right}$是第二等级的非支配前沿;而在多任务优化中,$\left{p_1,p_2,p_5,p_6\right}»\left{p_3,p_4\right}$,即在多任务优化中,$\left{p_1,p_2,p_5,p_6\right}$是不可比较的,因此在个体的评价上,EMOO和EMTO有很大的区别。
二、多因子进化算法(MFEA,MULTIFACTORIAL EVOLUTIONARY ALGORITHM)
2.1 定义
MFEA创造了一个多任务的环境,进化出一个单一的个体群体来同时解决多个任务,其中每个任务(有自己的目标)作为一个独特的文化因素来影响群体的进化。不同的任务可能具有不同的属性,因此可能导致个体的不同表示。因此,需要一种统一的表示方法,使所有任务的解空间可以方便地编码为相同的表示方法,以便搜索,并将其解码为唯一的表示方法,以便求值。MFEA提出了一种统一的表示方案,其中每个变量都由0和1之间的随机密钥编码,从而实现了对这种通用性的追求。
给出了一个由k个分量任务组成的MTO问题,MFEA产生n个个体的单个种群,即$pop=\left\{ p_i\right\}^n_{i=1}$,其同时搜索每个k分量任务的全局最优解。
定义1(Factorial Cost):个体$p_i$在任务$T_j$上的因子代价$\Psi_i^j$定义为$\Psi_i^j=\lambda \cdot \delta^j_i+f_i^j$,这里$\lambda$是一个惩罚因子,并且$\delta^j_i$和$f_i^j$定义为个体$p_i$在任务$T_j$上约束违反总数和目标函数值。
定义2(Factorial Rank):个体$p_i$在任务$T_j$上的因子等级$r_i^j$定义为按照因子代价升序排序之后的种群列表里$p_i $的索引。当多个个体具有相同的因子代价时,采用random tie-breaking方法。
定义3(Scalar Fitness):个体$p_i$的标量适应度$\varphi i$定义为$\varphi _i=1/min{j\in \left{1,…,k\right}}\left{ r_i^j \right}$。
定义4(Skill Factor):个体$p_i$的技能因素$\tau_i$定义为个人在所有任务中表现出最高能力的任务的索引,即$\tau i=argmin{j\in \left{1,…,k\right}}\left{ r_i^j \right}$。
定义5(Multifactorial Optimality):当且仅当个体$p^o $是所有k个组件任务中的全局最优值。,那么称其是多因素最优的。
2.2 思想
MFEA利用群体成员的技能因素隐式地将群体划分为k个不重叠的任务组,每个组专注于一个特定的任务,该任务由所有相同技能因素的成员组成。在此基础上,通过两个算法模块实现了知识转移——选择性交配(assortative mating)和选择性模仿(selective imitation),它们协同运作从而允许知识转移到不同的任务组。具体来说,选择性交配允许两个具有不同技能因素的个体(因此属于不同的任务组)在一定的概率下(通过交叉操作)交配,该概率由算法参数$rmp$控制,产生两个后代。然后,每一个产生的后代通过继承父母的技能因素来模仿父母中的任何一方,并仅仅对与继承的技能因素相对应的任务进行评估,这就是选择性模仿的作用。其次,每个继承技能因素的子代都与任务组的现有成员竞争以进入该任务组。通过利用这两个算法模块,MFEA可以从父母和后代两个方面控制跨任务的知识转移。MFEA的算法结构如下: ```javascript 1.生成初始个体种群并将其存储在current-pop (P)中; 2.根据多任务环境中的每个优化任务对每个个体进行评估; 3.计算每个人的技能因素; 4.while (停止条件不满足) do
a.在current-pop(P)上使用遗传算子生成offspring-pop(C),参见算法1;
b.仅在选定的优化任务上评估offspring-pop(C)中的个体,参见算法2;
c.合并P和C,组成一个新种群intermediate-pop(P∪C);
d.更新P∪C中的每个个体的标量适应度( )和技能因素( );
e. 从P∪C中选择适应度最高的个体,组成下一个current-pop(P); 5.end while ``` 其matlab代码如下: ```java % 本程序主要实现了进化多任务优化、优化函数为最小化函数、最大化函数需要转化为最小化函数 % 有任何问题可以联系我的邮箱: wangchao(Email: xiaofengxd@126.com)
clc,clear tic %% 参数设置 global N gen N = 30; % 种群大小(设置为偶数) rmp = 0.3; % 随机交配池概率 pi_l = 1; % 个体学习的概率(BFGA quasi-Newton Algorithm) Pc = 1; % 模拟二进制交叉概率 mu = 10; % 模拟二进制交叉参数(可调) sigma = 0.02; % 高斯变异模型的标准差(可调) gen = 100; %迭代次数 selection_process = ‘roulette wheel’; % 可供选择:elitist、roulette wheel、Tournament name = ‘RastriginRastrigin’; % 测试任务选择有:RastriginAckley、SphereWeierstrass、RastriginAckleySphere、RastriginRastrigin、AckleyAckley options = optimoptions(@fminunc,’Display’,’off’,’Algorithm’,’quasi-newton’,’MaxIter’,5); %调用matlab函数优化器(拟牛顿法)->设置预学习优化器
%% 初始化任务 Task = TASK(); Task = initTASK(Task,name);
%% MFEA %%% 0.记录最优解的矩阵 EvBestFitness = zeros(gen+1,Task.M); %每代最好的适应度值 TotalEvaluations=zeros(gen+1,1); %每代每个个体评价次数
%%% 1.初始化种群 Population = INDIVIDUAL(); %生成初始种群 Population = initPOP(Population,N,Task.D_multitask,Task.M);
%%% 2.根据多任务环境中的每个优化任务评估每个个体的因子代价 [Population,TotalEvaluations(1)] = evaluate(Population,Task,pi_l,options);
%%% 3.计算初始化种群的因素等级以及技能因素 [Population,EvBestFitness(1,:),bestind] = Calfactor(Population);
%%% 4.优化过程 for i = 1:gen %4.1 个体变异交叉 Offspring = GA(Population,rmp,Pc,mu,sigma); %4.2 计算因子代价 [Offspring,TotalEvaluations(i+1)] = evaluate(Offspring,Task,pi_l,options); TotalEvaluations(i+1) = TotalEvaluations(i+1) + TotalEvaluations(i); %4.3 种群合并 intpopulation = combpop(Population,Offspring); %4.4 更新标量适应度,技能因素,因素等级 [intpopulation,EvBestFitness(i+1,:),bestind] = Calfactor(intpopulation); %4.5 环境选择 Population = EnvironmentalSelection(intpopulation,selection_process,N,Task.M); disp([‘MFEA Generation = ‘, num2str(i), ‘ EvBestFitness = ‘, num2str(EvBestFitness(i+1,:))]);%为了记录初始化的值所以次数+1 end
%% 记录算法结果 data_MFEA.wall_clock_time=toc; data_MFEA.EvBestFitness=EvBestFitness; data_MFEA.bestInd_data=bestind; data_MFEA.TotalEvaluations=TotalEvaluations; save([‘Data',’data.mat’],’data_MFEA’);
%% 画图 for i=1:Task.M figure(i) hold on plot(EvBestFitness(:,i)); xlabel(‘GENERATIONS’); ylabel([‘TASK ‘, num2str(i), ‘ OBJECTIVE’]); saveas(gcf,[‘Data\figure_Task’,num2str(i),’.jpg’]); end
### 2.3 流程
#### 2.3.1 种群初始化
假设同时执行K个优化任务,第j个任务的维数由$D_j$给出。因此,我们定义了一个具有维数的统一搜索空间($D_{multitask}=max_jD_j$)。在种群初始化步骤中,每个个体都被赋予了一个由$D_{multitask}$随机变量组成的向量(每个变量都位于固定范围内$[0,1]$)。这个向量构成染色体(完整的遗传物质)。本质上,统一搜索空间的第i维由一个随机的key值$y_i$表示并且固定范围代表了统一空间的box-constraint。当处理任务$T_j $时,我们简单的引用染色体的第一个$D_j $的随机key。这样设计的主要原因为
1)从实用的角度来看,当同时解决多个具有多维搜索空间的任务时,它有助于规避与维数诅咒相关的挑战。
2)从理论上讲,它被认为是一种有效的基于种群的搜索功能的访问方法。其以一种有效的方式发现和隐式地将有用的遗传物质从一项任务转移到另一项任务。此外,由于群体中的单个个体可能会继承多个优化任务对应的遗传构建块,因此将其与多因子遗传进行类比就更有意义了。
其matlab代码如下:
```java
classdef INDIVIDUAL
%此类代表一个种群,由五个矩阵组成:染色体、因素代价、因素等级、标量适应度、技能因素,横—种群大小,纵—维度/任务数
%种群需要由initPOP初始化,评价种群个体时需要evaluate函数
properties
rnvec; % (genotype)--> decode to find design variables --> (phenotype)
factorial_costs;%因素代价
factorial_ranks;%因素等级
scalar_fitness;%标量适应度
skill_factor;%技能因素
end
methods
function object = initPOP(object,N,D,MM)
object.rnvec = rand(N,D);%初始化个体编码
object.factorial_costs = inf*ones(N,MM);%初始化个体因素代价为0
object.factorial_ranks = zeros(N,MM);%初始化个体因素等级为0
object.scalar_fitness = zeros(N,1);%初始化个体标量适应度为0
object.skill_factor = zeros(N,1);%初始化个体的技能因子为0
end
function [object,call] = evaluate(object,Task,pi_l,options)%适应度评价
object.factorial_costs(:)=inf;
call = 0;
for i = 1:Task.M
[object.factorial_costs(:,i),object.rnvec,calls]=CalObj(Task,object.rnvec,pi_l,options,i,object.skill_factor);
call = call + calls;
end
end
end
end
2.3.2 遗传机制
MFEA的一个关键特征是,两个随机选择的亲本候选人必须满足一定的条件才能进行交叉。遵循的原则是非随机或assortative mating,它表明个体更喜欢与那些相同的文化背景的交配。MFEA里技能因素($\tau$)代表个体的文化偏见。因此,两个随机选择的父母候选人可以自由地进行交叉,如果他们拥有相同的技能因素。相反,如果他们的技能因素不同,在一个规定的随机交配概率($rmp$)或其他突变方式进行交叉。此算法中使用参数$rmp$来平衡搜索空间的开销和探索。接近0的$rmp$值意味着只有在文化上相似的个体才允许跨界,而接近1的值则允许完全随机交配,实际上在rmp更大的值(接近1)下发生的跨文化交配增加了对整个搜索空间的探索,从而有助于逃离局部优化,因此$rmp$是个至关重要的参数。算法2提供了根据这些规则创建后代的步骤。 ```javascript 1.考虑从current-pop中随机选择的两个父候选pa和pb; 2. 生成一个介于0和1之间的随机数rand; 3. if ( == ) or (rand < rmp) then
a. 父母pa和pb交叉得到两个后代个体ca和cb。; 4.else
a. 亲本pa发生了轻微的突变,从而产生了后代ca;
b. 亲本pb发生了轻微的突变,产生了一个子代cb; 5.end if ``` 其matlab代码如下: ```java function Offspring = GA(Parent,rmp,Pc,disC,sigma) % 此函数功能是通过模拟二进制交叉和高斯变异产生子代,并利用垂直文化传播进行技能因子的继承(两两组成的父代个体,必须进行交叉或者变异)。 % Input: Parent父代信息(染色体,技能因子)、rmp文化交流参数、Pc模拟二进制交叉概率、disC交叉参数、sigma高斯变异参数 % Output: Offspring子代信息(染色体,技能因子) % 第“1.”模式中,通过变异产生的两个后代可能具有相同的父母;第“2.”模式中,通过变异产生的两个后代父母一定不同
[N,~] = size(Parent.rnvec);
select = randperm(N);
rrnvec = Parent.rnvec(select,:);%打乱顺序
sskill_factor = Parent.skill_factor(select,:);
Parent1 = rrnvec(1:floor(end/2),:);
factor1 = sskill_factor(1:floor(end/2),:);
Parent2 = rrnvec(floor(end/2)+1:floor(end/2)*2,:);
factor2 = sskill_factor(floor(end/2)+1:floor(end/2)*2,:);
Offspring = INDIVIDUAL();
%Offspring.skill_factor = zeros(N,1);%1.初始化子代的技能因子为0
Offspring.skill_factor = sskill_factor;%2.初始化子代的技能因子对应为父代的技能因子
factorb1 = repmat(1:N/2,1,2);
factorb2 = repmat(N/2+1:N,1,2);
temp = randi(2,1,N);%对于子代随机选择它是继承第一个父母还是第二个父母
offactor = zeros(1,N);
offactor(temp == 1) = factorb1(temp == 1);
offactor(temp == 2) = factorb2(temp == 2);%子代继承父母的编号
%Offspring.skill_factor = sskill_factor(offactor);%1.所有子代继承父代基因
[NN,D] = size(Parent1);
% Simulated binary crossover
beta = zeros(NN,D);
mu = rand(NN,D);
beta(mu<=0.5) = (2*mu(mu<=0.5)).^(1/(disC+1));
beta(mu>0.5) = (2-2*mu(mu>0.5)).^(-1/(disC+1)); % beta = beta.*(-1).^randi([0,1],N,D); % beta(rand(N,D)<0.5) = 1;
beta(repmat(factor1 ~= factor2 & rand(NN,1)>=rmp,1,D)) = 1;%不同技能因子的个体只有满足rmp才能交叉
beta(repmat(rand(NN,1)>=Pc,1,D)) = 1;
Offspring.rnvec = [(Parent1+Parent2)/2+beta.*(Parent1-Parent2)/2
(Parent1+Parent2)/2-beta.*(Parent1-Parent2)/2];
Offspring.skill_factor(repmat(beta(:,1) ~= 1,2,1)) = sskill_factor(offactor(repmat(beta(:,1) ~= 1,2,1)));%2.对于交叉的个体,其随机选择一个父代继承基因。
% mutation
rvec=normrnd(0,sigma,[N,D]); % temp1 = Offspring.rnvec(offactor,:);1. % Offspring.rnvec(repmat(beta(:,1) == 1,2,D)) = temp1(repmat(beta(:,1) == 1,2,D)) + rvec(repmat(beta(:,1) == 1,2,D));%1.只对没有交叉的个体进行变异
Offspring.rnvec(repmat(beta(:,1) == 1,2,D)) = Offspring.rnvec(repmat(beta(:,1) == 1,2,D)) + rvec(repmat(beta(:,1) == 1,2,D));%2.只对没有交叉的个体进行变异
Offspring.rnvec(Offspring.rnvec>1)=1;
Offspring.rnvec(Offspring.rnvec<0)=0; end ``` #### 2.3.3 选择性评价
在评价第$i$个个体的第$j$个任务时,第一步是先将染色体的键值解码成有实际意义的输入。也就是说,随机键值表示作为一个统一的搜索空间,从这个空间可以推导出属于问题解的表示。对于连续优化而言,假设第$i$维变量的$x_i$的边界为$L_i,U_i$,此个体的键值为$y_i$,那么$x_i=L_i+(U_i-L_i)*y_i$。在离散优化的情况下,染色体解码方案通常是依赖于问题本身。
如果对每个个体的每个任务都进行评估,显然计算量会很大,因此为了使MFO更实用,MFEA必须设计的高效。易知,一个个体很难在所有任务上都表现的出色,因此,理想情况下,可以只针对最有可能出色执行的任务对个人进行评估,算法3给出这一观点的具体实施措施,它允许后代模仿任何一个父母的技能因素(文化特征),这种方式大大减少了评估次数。 ```java 一个子代c要么有两个父代(pa和pb)要么只有一个父代(pa或pb)——参见算法1; 1. if (‘c’ 有两个父代) then
a.生成一个介于0和1之间的随机数rand;
b. if (rand<0.5) then
“c”模仿pa,且子代只在任务 (pa的技能因素)上评估;
c. else
“c”模仿pb,且子代只在任务 (pb的技能因素)上评估;
d. end if 2.else
a. “c”模仿其唯一的父代,且子代只在其父代技能因素对应的任务上评估; 3.end if ``` #### 2.3.4 遗传算子
为了确保算法收敛并且保留每代优秀的解,MFEA采用精英保留策略。交叉算子选择模拟二进制交叉(SBX),变异算子选择高斯变异。
在多任务算法中,从直觉上看随机产生的或经过基因改造的个体更有可能胜任至少一项任务。MFEA的机制建立在这一观察的基础上,它将人群有效地划分为不同的技能组,每个人都擅长于不同的任务。更好玩的是在一个特定群体中产生的遗传物质也可能对另一项任务有用。因此跨任务的遗传转移可能会潜在的导致很难找到全局最优。在MFEA中,通过偶尔的染色体交叉,允许不同的技能群体相互交流,从而促进遗传物质的转移。因此MFEA主要利用了群体的相互交流以及文化的垂直传播,即$rmp$操作和后代模仿父母的技能因素。
三、实验
在设计的实验中,每一个任务都是一个待解决的优化问题,通过数值实验说明了MFEA的有效性。
3.1 目标任务函数
1.Sphere函数 \(\sum_{i=1}^Dx^2_i\) 2.Ackley函数 \(20+e-20e^{-0.2\sqrt{\frac{1}{D}\sum_{i=1}^Dz_i^2}}-e^{\frac{1}{D}\sum_{i=1}^Dcos(2\pi z_i)};z=M_R\times(x-O_A)\) 3.Rastrigin函数 \(\sum_{i=1}^D(z_i^2-10cos(2\pi z_i)+10);z=M_R\times(x-O_R)\) 这里$M_A$和$M_R$是随机生成的旋转矩阵。而且$O_A$和$O_R$是各自对应函数的全局最优。
Sphere函数的复杂性最低,而多模态的Rastrigin函数的优化具有较大的挑战性。
此次实验共分为两组,第一组包含三个两任务优化问题,一个单任务优化问题;第二组包含四个两任务优化问题,一个单任务优化问题。我们考虑20个和30个变量的函数,为了方便表示,这里将问题维数和函数名首写字母联合表示一个任务。具体如下所示:
$F1:\left{ (30R,none),(30R,30S),(30R,30A),(30R,20S) \right}$;$F2:\left{ (30A,none),(30A,30S),(30A,30R),(30A,20S),(30A,20R) \right}$。
这里(:,:)代表一个多任务优化问题,如果是单任务优化问题,括号的后半部分设为$none$。 其matlab代码如下:
function obj = Ackley(var,MM)
%Ackley函数,MM为随机生成的旋转矩阵
dim = length(MM);
var = var(:,1:dim);
[NN,dim] = size(var);
opt=0*ones(NN,dim);
var = (MM*(var-opt)')';
obj = 20 + exp(1) - 20*exp(-0.2*sqrt((1/dim)*sum(var.^2,2))) - exp((1/dim)*sum(cos(2*pi*var),2));
end
function obj = Rastrigin(var,MM)
%Rastrigin函数,MM为随机旋转矩阵
dim = length(MM);
var = var(:,1:dim);
[NN,dim] = size(var);
opt=0*ones(NN,dim);
var = (MM*(var-opt)')';
obj = 10*dim + sum(var.^2-10*cos(2*pi*var),2);
end
function obj = Sphere(var,MM)
%Sphere函数,MM为随机旋转矩阵
dim = length(MM);
var = var(:,1:dim);
[NN,dim] = size(var);
opt=0*ones(NN,dim);
var = (var - opt);
obj=sum(var.^2,2);
end
3.2 实验设置
为了确保确实存在一些有用的遗传物质,可以从一个问题转移到另一个问题,因此假设实验中所有搜索空间的每个维度范围为[-50,50]。本此实验给出的所有结果都是在一致的实验设置下,对每个问题集进行了5次独立运行。种群大小设置为30,最大运行代数设置为100。除此之外,为了获得高质量的解,每个个体都要进行预学习,对于连续问题而言,采用BFGS拟牛顿法进行个体学习。为了让文化交流更加充分,$rmp$设置为0.3。
3.3实验结果
根据3.3的实验设置,得到实验结果如图2所示。 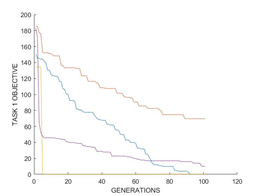
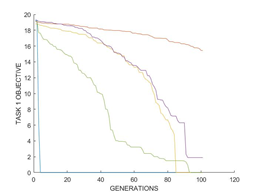
从图2(a)中可知,多任务处理的大多数实例都显著提高了收敛速度。因为Sphere函数在搜索过程中得到了瞬时的优化,从而产生了用于优化Rastrigin函数的精细遗传物质,(30R,30S)在前几代就已经收敛了。尽管Ackley的函数是多模态的,但由于其局部最优性较浅,优化难度较小。因此在实验(30R, 30A)中,Ackley的函数趋于较快的收敛,使得高质量的遗传物质可以转移到Rastrigin的函数中,从而快速收敛。最后,在问题(30R, 20S)中,Sphere函数时产生的遗传物质只占Rastrigin函数所需的$\frac{2}{3}$,因此收敛速度收到了限制,但依旧优于(30R, none)的整体性能。
图2(b)的收敛特征与图2(a)相似。由曲线(30A, none)和(30A, 30R)可以发现,Rastrigin函数也会导致Ackley函数的加速收敛。Rastrigin函数实际上更难优化,因此预计其会减慢收敛速度。但相反,在规定的基因交换中,MFEA却有助于两种任务的融合,从而使进化中的种群成功地同时利用了这两种函数,从而有效地绕过障碍,更快地收敛。
四、结论
本算法将多任务处理引入了优化领域,并取得了不错的效果。可以看出:该算法具有统一的染色体表示方案,是处理跨域多任务问题的关键;隐式遗传从简单任务转移到复杂任务,并且在遗传互补的存在下,可以使复杂优化任务快速收敛;两个复杂任务之间的遗传交换有利于同时探索这两个函数,从而有效地避开障碍,加快收敛;利用文化传播的自然现象,在多因素设置下,可以潜在地减少了优化算法的运行时间。
通过对跨域多任务处理中个体任务收敛特性的深入分析表明,虽然某些任务受到内隐遗传转移的正向影响,但也可能存在某些任务受到负向影响。然而,在大多数情况下,正迁移大于负迁移,因此当对所有任务的性能取平均时,将导致收敛趋势。
在现实生活中,一个复杂问题常常由几个相互依赖的子问题组成,MFO可以同时解决这些问题,但是当问题的优先级受到限制,这意味着某些任务必须利用某些其他任务的结果,那么MFO就不再适用了,因此设计新的处理MFO的算法有重要的意义。 ## 五、参考文献 [1] A. Gupta, Y.-S. Ong, and L. Feng, “Multifactorial evolution: Toward evolutionary multitasking,” IEEE Trans. Evol. Comput., vol. 20, no. 3, pp.343–357, 2016.
算法的完整代码见进我CSDN主页即可下载,代码里面借鉴了很多原作者和田野老师platEMO平台上的算子操作,在此表示感谢。注:代码里的所有文件夹必须添加到matlab的路径中才可以运行哦!
Comments
😅 Commenting is disabled on this post.